Ako ste na tom s vnímaním pravdepodobnosti? Otestujte sa v troch jednoduchých problémoch 🙂
1. Problém troch dverí (problém Montyho Halla)
Zadanie
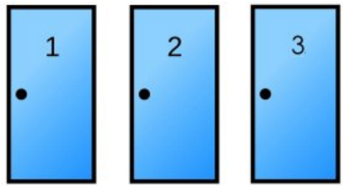
Máte pred sebou 3 dvere. Za jednými z nich je ukrytá hlavná cena – auto. Zvyšné dvoje dvier ukrývajú iba cenu útechy – kozu. Vašim cieľom je samozrejme vyhrať auto. Úloha má 3 kroky.
1. V prvom kroku si vyberiete jedny z dverí a postavíte sa k nim (napríklad si vyberiete dvere číslo 2)
2. Moderátor následne otvorí jedny dvere, za ktorými je koza (na obrázku sú to dvere číslo 3). Zatvorené tak ostanú už iba dvere číslo 1 a 2. Pred jednými z nich stojíte
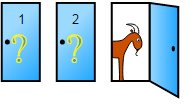
3. Moderátor vám následne ponúkne možnosť svoj výber zmeniť. Môžete teda ostať stáť pred dverami, ktoré ste si vybrali v prvom kroku, alebo prejsť k tým druhým. Ihneď po vašom rozhodnutí moderátor otvorí dvere 1 aj 2 a vy sa dozviete, čo ste vyhrali.
Otázka: Aká stratégia v treťom kroku dáva najväčšiu pravdepodobnosť na výhru auta?
- Zmeniť dvere
- Nezmeniť dvere
- Je to jedno
Riešenie
Intuitívna odpoveď je pomerne jednoznačná – „je to jedno“. Vychádza z predpokladu, že v treťom kroku sú k dispozícii už iba dvoje dvere a tak je šanca na výhru 50:50. Táto odpoveď je však nesprávna. Najlepšou stratégiou je vždy dvere zmeniť. Táto stratégia dáva 66% šancu na výhru auta. Ak sa rozhodnete dvere nemeniť, vaša šanca na výhru je iba 33%.
Správna odpoveď vychádza z kroku 1. V ňom si vyberáte 1 z 3 dverí, máte teda 33% šancu na to, že si v prvom kroku vyberiete auto a 66% šancu na to, že si vyberiete kozu. Ak teda budete hrať stratégiou „nezmeniť“, musíte si auto vybrať už v prvom kole. Vaša šanca na výhru je tak 33%. Na druhej strane, ak budete hrať stratégiu „zmeniť“, tak pre výhru auta potrebujete v prvom kole vybrať kozu. A keďže až 2 z 3 dverí ukrývajú kozu, vaša šanca na výhru auta je 66%.
Problém Montyho Halla je známy už veľmi dlho a na internete môžete nájsť množstvo objasňujúcich textov a videí. Jedno z nich napríklad tu:
Ak stále neveríte, môžete si hru vyskúšať hoci aj 1000 krát na tomto odkaze 🙂
http://www.shodor.org/interactivate/activities/SimpleMontyHall/
2. Paradox istej vs. neistej výhry
Predstavte si, že dostanete šancu zasúťažiť si o peniaze v dvoch hrách. V oboch hrách budete mať na výber z dvoch možností. Ako sa rozhodnete?
Hra 1
Možnosť 1: 20% šanca na výhru 4000 EUR
Možnosť 2: 25% šanca na výhru 3000 EUR
Ktorá možnosť v Hre 1 je pre vás lákavejšia?
Hra 2
Hra 2 je dvojkolová. V prvom kole je 75% šanca, že hra sa okamžite ukončí a vy nevyhráte nič a 25% šanca na postup do druhého kola. Ak sa dostanete do druhého kola, dostanete na výber z dvoch možností:
Možnosť 1: 80% šanca na výhru 4000 EUR
Možnosť 2: Istých 3000 EUR.
Rozhodnutie musíte urobiť ešte pred prvým kolom.
Ktorá možnosť v Hre 2 je pre vás lákavejšia?
Riešenie
Tento paradox uviedli v roku 1979 D. Kahneman a A. Tversky. Hry nemajú žiadne správne ani nesprávne riešenie, samozrejme, voľba je vždy otázkou osobných preferencií. U väčšiny ľudí je však možné pozorovať istý paradox. Totiž, ak patríte k väčšine (spolu so mnou), tak je pre vás v Hre 1 atraktívnejšia Možnosť 1 a v Hre 2 zase Možnosť 2. To však z matematického pohľadu nedáva veľký zmysel, keďže hry sú úplne rovnaké. Kľúčom k pochopeniu je prvé kolo Hry 2. Keďže šanca na postup do druhého kola je iba štvrtinová, v podstate to znamená, že v Hre 2 je z pohľadu celkových šancí na úspech 0,25*0,8 = 0,2, teda 20% šanca na výhru v 4000 EUR pre Možnosť 1 a 0,25*1=0,25, teda 25% šanca na výhru 3000 EUR pre Možnosť 2.
Voľby v Hre 1 a Hre 2 sú tak úplne identické. Napriek tomu drvivá väčšina ľudí vyberá v Hre 2 opačnú možnosť ako v Hre 1. Prvé kolo Hry 2 je tak efektívne ignorované. Tento paradox ukazuje, ako jednoducho je možné manipulovať s ľuďmi, pokiaľ ide o neisté javy. V podstate stačí nalepiť na seba dve neisté udalosti a podať ich vo „vhodnom“ znení. Alebo ponúknuť zdanlivú „istotu“.
3. Problém spoľahlivosti testu
Zadanie
Predstavte si chorobu, ktorú má presne 1% populácie. Táto choroba sa navonok nijako neprejavuje, nikto teda nevie, či chorobu má alebo nie. Pre chorobu však existuje chemický test, ktorého spoľahlivosť je 99%. Test teda v 99% prípadov správne určí, či človek chorobu má alebo nie a v 1% prípadov sa pomýli.
Keďže sa o chorobu zaujímate, rozhodnete sa nechať sa testovať. Výsledok testu hovorí, že chorobu máte.
Otázka
Aká je pravdepodobnosť, že chorobu skutočne máte?
Riešenie
Intuitívna odpoveď na túto otázku je 99%. Vyznieva to logicky. Ak je spoľahlivosť testu 99% a test mi ukázal, že som chorý, potom som chorý s pravdepodobnosťou 99%. To však nie je pravda. V skutočnosti je to „iba“ 50%. Pre vypočítanie správneho riešenia je totiž potrebné zobrať do úvahy aj možnosť, že som zdravý a test mi chybne označil chorobu.
Skúsme si to ukázať na konkrétnych číslach. Majme milión ľudí, z ktorých 1% má chorobu, čo dáva 990 000 zdravých a 10 000 chorých. Povedzme, že budeme testovať všetkých z nich. Testy teda dopadnú nasledovne:
| Stav | Test ukáže | Počet |
| Chorý
(10 000 ľudí) |
Chorý (99%) | 9 900 |
| Zdravý (1%) | 100 | |
| Zdravý
(990 000 ľudí) |
Chorý (1%) | 9 900 |
| Zdravý (99%) | 980 100 |
Test zistí chorobu u 19 800 ľudí, ale z nich ju aj naozaj má iba 9 900 (teda 10 000 mínus 100 – to sú tí, ktorí síce chorí sú, ale test im to neukázal). Skutočná pravdepodobnosť, že máte chorobu, ktorú vám tento test zistil je teda iba 50%. Inými slovami, každý druhý človek z tých, ktorým bola nájdená choroba je v skutočnosti zdravý.
Záver
Tri problémy, ktoré som v blogu predstavil sa na prvý pohľad môžu zdať iba ako triviálne matematické hračky, ktoré toho nemajú s reálnym svetom veľa spoločného. V skutočnosti však žijeme vo svete, v ktorom je takmer každá udalosť neistá a v mnohých prípadoch sa rôzne javy navzájom podmieňujú a ovplyvňujú. Naša intuícia však nedokáže spoľahlivo pracovať s podmienenými pravdepodobnosťami a keďže drvivú väčšinu rozhodnutí robíme práve intuitívne, je tu až desivo veľký priestor na manipuláciu. A tým naozaj nechcem povedať, že tu takáto manipulácia ešte nie je…
Moja FB stránka:
